严刑能遏制腐败吗？（5）

按照上述思路，本文构建了一个类似于塞贝利斯的犯罪与惩罚模型的博弈。塞贝利斯试图寻求博弈中六种情形下的纳什均衡：1.完全信息（博弈双方清楚彼此的收益）、理性、连续策略、同时行动；2.完全信息、理性、离散策略、同时行动；3.完全信息、理性、连续策略、先后行动（在行为选择上，博弈者1先决定是腐败还是清廉，博弈者2再选择是否查处）；4.适应性行为、交替行动（即没有一方是完全理性的，双方都是适应性行为、交替行动）；5.双方信息都是不完全的（每个博弈者只知道自己的收益情况而不知道对方的）、理性、离散策略、同时行动；6.一方信息不完全（其中一方的收益为双方所知道，而另一方的收益是随机的）、理性、离散策略、同时行动。他证实了六种情况下的均衡是一样的，即双方都选择混合策略。假设腐败查处的概率为p,下级官员腐败的概率为q，则有：

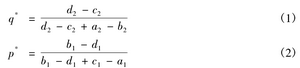
有趣的是，双方的均衡策略q* 和p*，完全取决于对方的收益，而不是自身的收益。这是因为在混合策略的纳什均衡里，双方做出的策略选择q和p，使对方在不同纯策略下的收益一样。因而可知，q和p完全是由对方的收益决定的。我们可以用下面两个定理把这个结论概述出来。

定理1：根据假设1至4，下属收益的变化不会改变其腐败的概率(q*)；但会影响书记对腐败查处的概率(p*)。

定理2：在假设1至4的情况下，书记收益的变化不会改变其查处腐败的概率(p*)；但会更多地影响其下属腐败的概率(q*)。

为了回答关键性问题：严刑能遏制腐败吗？我们从定理1中引申出了命题1（对命题1的证明详见原文附录A）。

命题1：对腐败处罚的加大将会降低书记查处腐败的概率(p*)，但不会降低其下属腐败的概率(q*)。

定理1、2和命题1听起来有违直觉。然而，这并不是数学游戏。我们通常认为一方收益的变化会引起其自身行为的变化，这种惯性思维实际上是有问题的。因为这种思维仅从下属官员一方的角度来考虑问题，忽略了腐败与反腐败其实是下属官员与其上级领导之间的相互博弈。

直觉上，更严厉的惩罚会在短期内对腐败官员有所震慑，他们的腐败行为也会有所收敛。在此情况下，书记会把用于督查腐败的投入转移到其他领域，对腐败的查处也不像先前那么频繁。随着时间的推移，一些官员腐败的苗头又会露出来。这种情形在一些发展中国家如中国尤其如此：一方面，腐败很严重，需要控制；另一方面，资源不足而且其他部门也迫切需要。因为对腐败的日常监督是有成本的，而且监督的边际收益也是逐渐递减的，因此一个资源受约束的国家更倾向于用严惩来遏制腐败，从而可以把资源用到其他更重要的事项上，比如经济发展。但是，正如上述模型所表明的，即使对腐败采取零容忍，仅靠严厉的惩罚也不足以减少腐败。更严厉的惩罚只会减少对腐败的查处。因此，中国刑法规定的极其严厉的惩罚如无期徒刑和死刑，对腐败的遏制作用是很低的。事实上，极刑可能是导致腐败低惩罚率的一个因素。还有没有其他办法能使惩罚降低腐败呢？定理2表明，为了降低腐败的发生率q*，必须改变书记的收益，比如提高a2（使腐败的查处更有利于书记）或者降低b2（对腐败的包庇使书记利益受损）。因此，为了控制腐败，我们不仅需要采取措施降低腐败的激励，还要增加腐败查处的激励。按照定理2，能使惩罚有效降低腐败的一个可行的办法就是使书记能从腐败的查处中获益更多。这一点表明我们需要将双方的收益挂钩。塞贝利斯讨论了假设的放松如何对最初结果产生影响。但是他没有放松基本的条件——每个人的收益彼此独立。下节将构建一个博弈双方利益相关的模型，并得出一些有益于中国反腐的政策建议。